
Exponential Distribution - Maximum Likelihood Estimation
 |
Exponential Distribution - Maximum Likelihood Estimation |
|
The following section describes maximum likelihood estimation for the normal distribution using the Reliability & Maintenance Analyst. The manual method is located here. The maximum likelihood estimation routine is considered the most accurate of the parameter estimation methods, but does not provide a visual goodness-of-fit test. It is recommended to verify goodness-of-fit using probability plotting or hazard plotting, and then, if the fit is acceptable, use maximum likelihood estimation to determine the parameters. Maximum likelihood estimation provides confidence limits for all parameters as well as for reliability and percentiles. To estimate the parameters of the normal distribution using maximum likelihood estimation, follow these steps:
The estimated parameters are given along with 90% confidence limits; an example using the data set "Demo2.dat" is shown below.
The default confidence level is 90%. The confidence level can be changed using the spin buttons, or by typing over the existing value. Changing the confidence level erases the confidence limits for the parameters. To re-calculate the confidence limits, click the "Compute Confidence Limits" button. Clicking the "Plot" button gives a plot of expected reliability with upper and lower confidence limits at the level specified. A plot of percentiles (time as a function of reliability) is produced by selecting the "Percentiles" option in the Plot Type frame before clicking the "Plot" button. The title of the graph can be changed by editing the text in the Graph Title frame. To check the spelling of the title, click the "Spell Check" button. To predict reliability or time-to-fail using the estimated parameters use the Predicting Module. Manual Maximum Likelihood Estimation The exponential probability density function is
The maximum likelihood estimation for the parameter q is
where xi is the ith data point; this may be a
failure or a censoring point, This estimate is unbiased and is the minimum variance estimator. Example 30,183 14,871 35,031 76,321 43,891 31,650 12,310 Assuming an exponential time to fail distribution, estimate the mean time to fail and the mean failure rate. Solution
The mean failure rate is the inverse of the mean time to fail
Click here to download this example in an Excel spreadsheet. Example: Solution: The mean time to fail is
The mean failure rate is l = 1/149,179.6 = 0.0000067 failures per cycle
For a time truncated test a confidence interval for q is
Note that the degrees of freedom differ for the upper and lower limits.
Example Solution
For a 90% confidence interval, a = 0.1; C2( 0.05,10) = 18.307, and C2( 0.95,10) = 2.733. The 90% confidence interval for q is
1,385.5<q<9280.6 The confidence interval for the failure rate is the inverse of the confidence interval for the mean time to fail. 0.0001077<l<0.0007217 Click here to download this example in an Excel spreadsheet.
For a failure truncated test and for multiple censored data, a confidence interval for q is
Note that the degrees of freedom are the same for the upper and lower limits.
Example Solution
For a 95% confidence interval, a = 0.05; C2( 0.025,10) = 20.483, and C2( 0.975,10) = 3.247. The 95% confidence interval for q is
145.3<q<916.5 Click here to download this example in an Excel spreadsheet.
For failure free testing the one sided lower confidence limit simplifies to
where t is the testing time,
Example 3.5 Solution 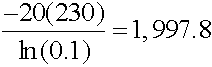 hours hours
A confidence interval for reliability is
where qL is the lower confidence limit
for the mean time to fail, and A confidence interval for percentiles is
where P is the probability of failure prior to time = x.
Example Solution
The lower 90% confidence limit for reliability at time = 1000 is
Click here to download this example in an Excel spreadsheet. |